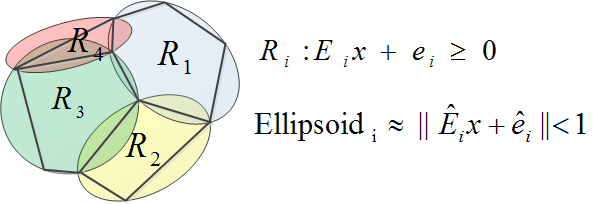Motivation

For controller design, consider the following issues:

Theory of Linear Systems is very rich in terms of analysis and synthesis methods and computational tools.

Real world systems, however, are usually nonlinear.

What can be done to extend the good properties of linear systems theory to nonlinear systems?

Gain scheduling is an attempt to address this issue

Divide and conquer

Approximating nonlinear systems by a combination of local linear systems

Designing local linear controllers and combining them

Started in 1960s, very popular in a variety of fields from aerospace to process control

Problem: proof of stability!

Problem: By switching between two stable linear system, you can create an unstable system.

Solution: Lyapunov based methods

Framework: Piecewise Smooth Systems

PWA Systems

Piecewise Smooth Systems

The dynamics of a piecewise smooth (PWS) is defined as:

\begin{equation*} \dot x=f_i(x),\ x\in\RC_i \end{equation*}

where \(x\in\XC\) is the state vector. A subset of the state space \(\XC\) is partitioned into \(M\) regions, \(\RC_i, i=1,\ldots,M\) such that:

\begin{equation*} \cup_{i=1}^M \bar\RC_i=\XC,\ \RC_i\cap\RC_j=\emptyset,\ i\neq j \end{equation*}

where \(\bar\RC_i\) denotes the closure of \(\RC_i\) .

PWA Systems

The dynamics of a piecewise affine (PWA) is defined as:

\begin{equation*} \dot x=A_ix+a_i+B_iu,\ x\in\RC_i \end{equation*}

where

\begin{equation*} \RC_i = \{x| E_ix+e_i\geq 0\},\ i=1,2,\ldots,M \end{equation*}

PWA systems are nonlinear.
PWA systems are locally linear.

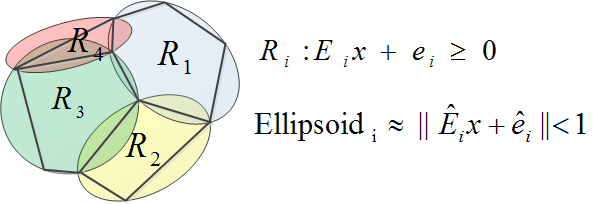
PWA Systems

PWA Slab Systems

The regions of PWA slab system are intervals on a scalar variable:

\begin{equation*} \RC_i=\{x|\beta_i<c^\TR x<\beta_{i+1}\} \end{equation*}

The regions of a PWA slab system can be written as degenerate ellipsoids:

\begin{equation*} \RC_i=\{x|\ |E_ix+e_i|<1 \} \end{equation*}

PWA Systems

PWA Differential Inclusions

In this toolbox, we have considered PWA differential inclusions (PWADI) described by:

\begin{equation*} \dot x \in \CO\{A_{i1}x+a_{i1}+B_{i1}u,A_{i2}x+a_{i2}+B_{i2}u\},\ x\in\RC_i \end{equation*}

PWADIs are a form of uncertain PWA systems.
Nonlinear systems can be included by PWADIs.

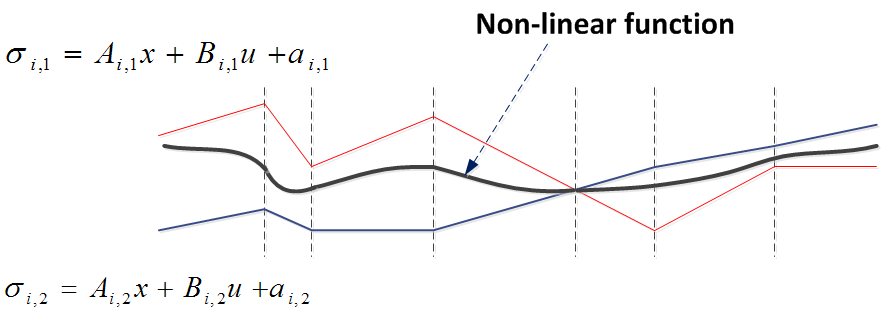
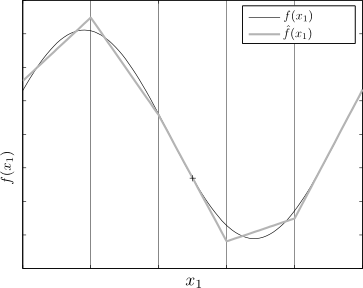
PWA Approximation

Given a nonlinear system:

\begin{equation*} \dot x = Ax+a+f(x)+B(x)u \end{equation*}

PWATOOLS can create a PWA approximation using the following approaches:

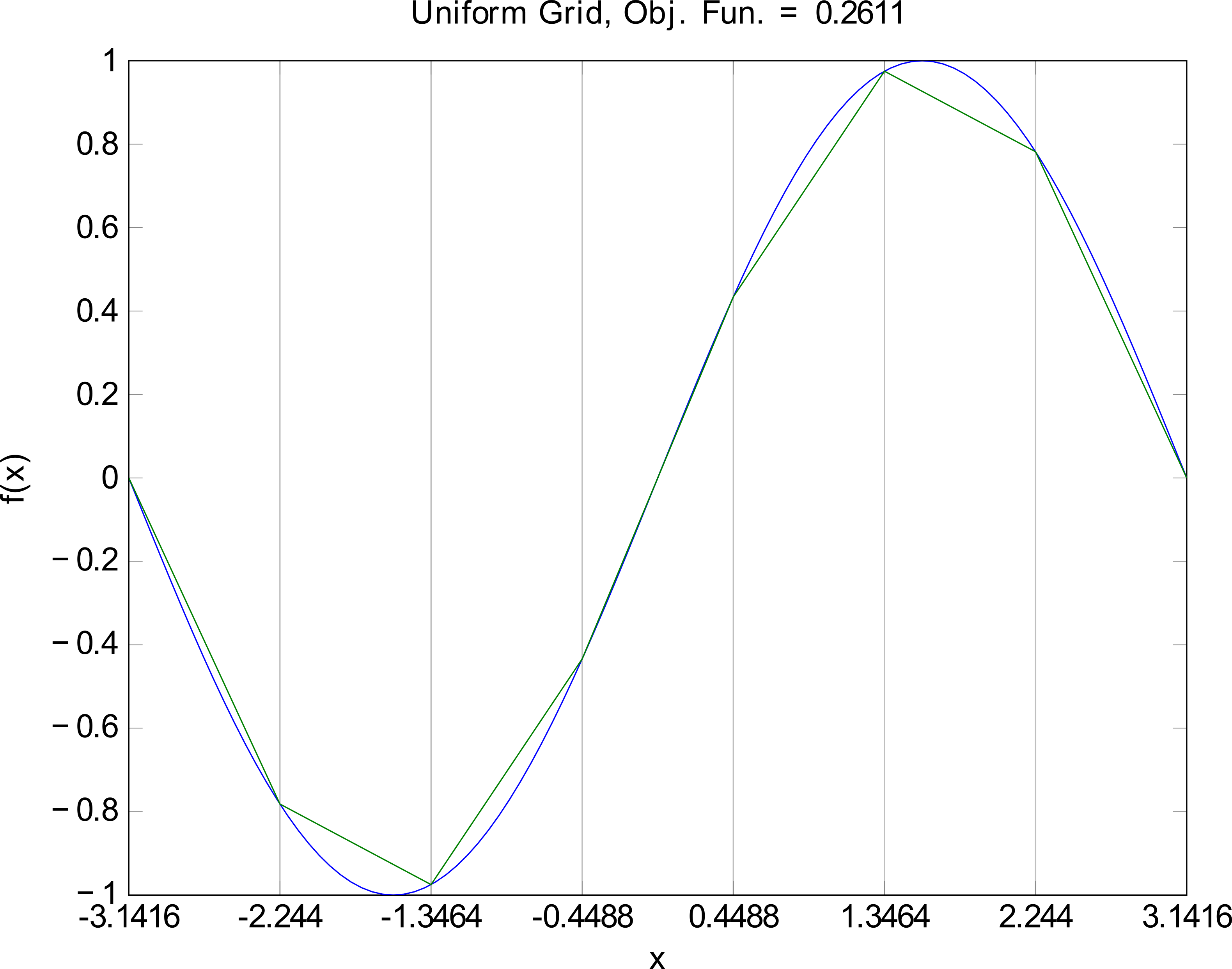
Uniform: connecting the dots of a uniform grid on the nonlinear surface
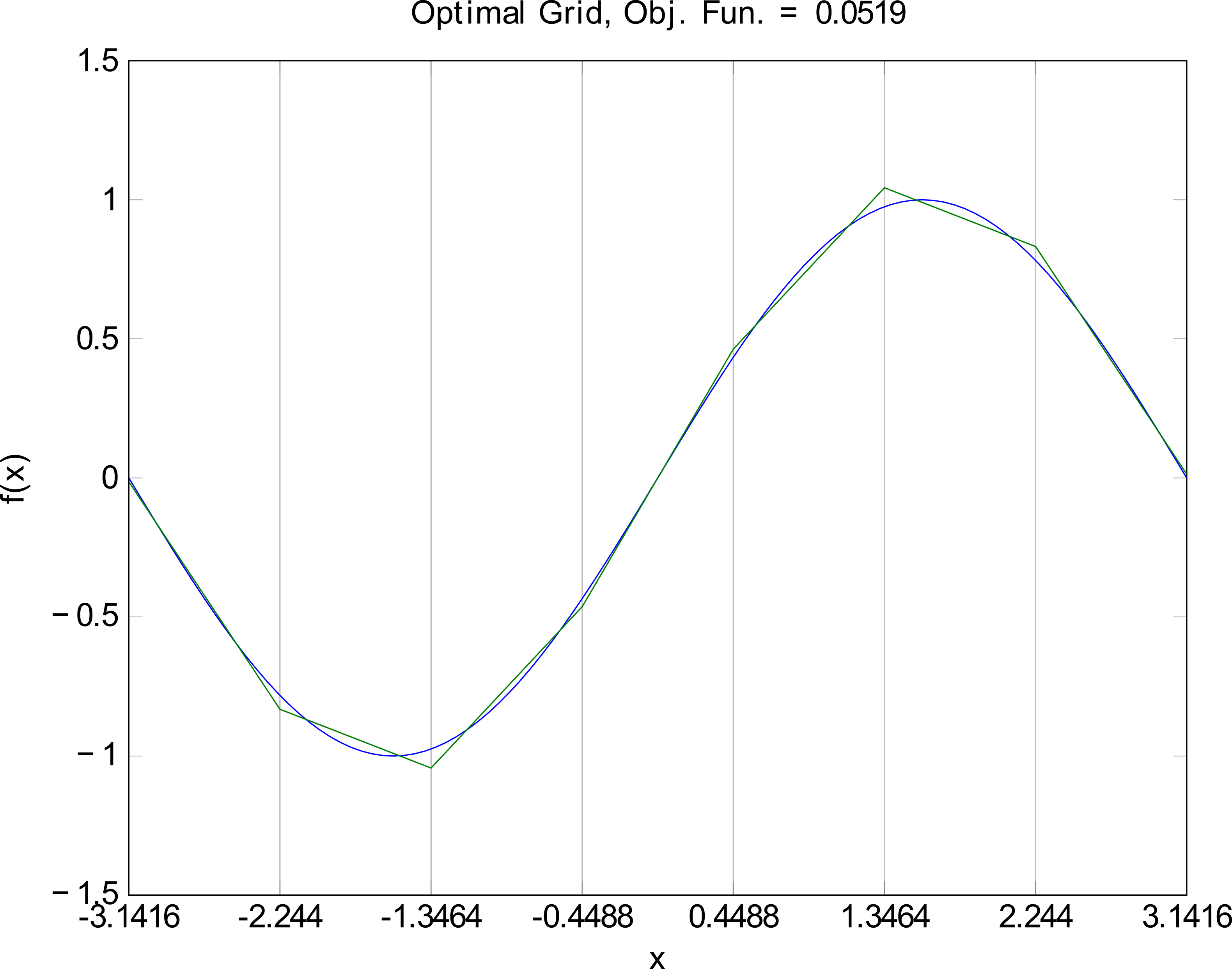
Optimal Uniform: minimizing the error for a uniform grid
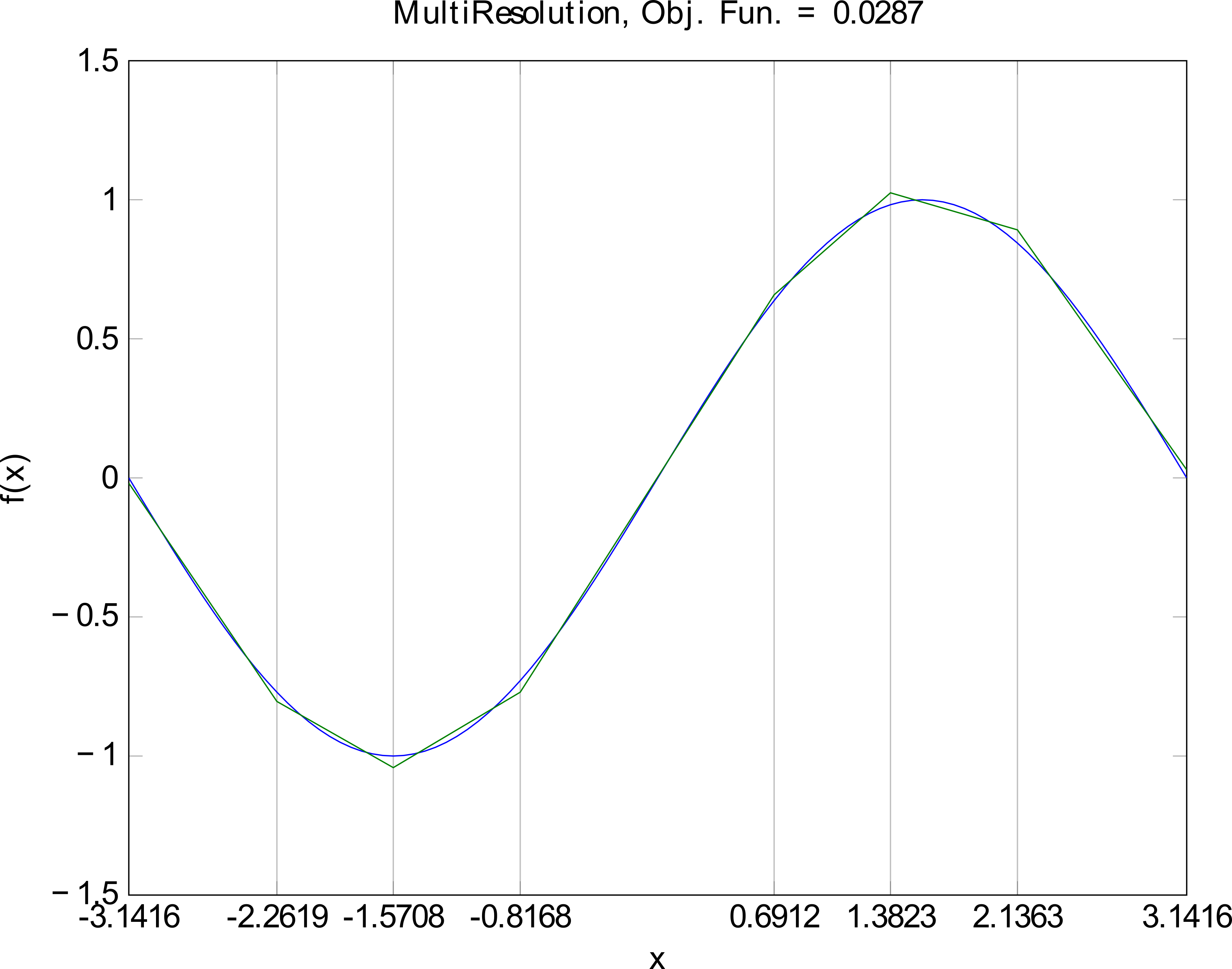
Multi-resolution: recursively building a nonuniform grid based on error minimization (divide and conquer)
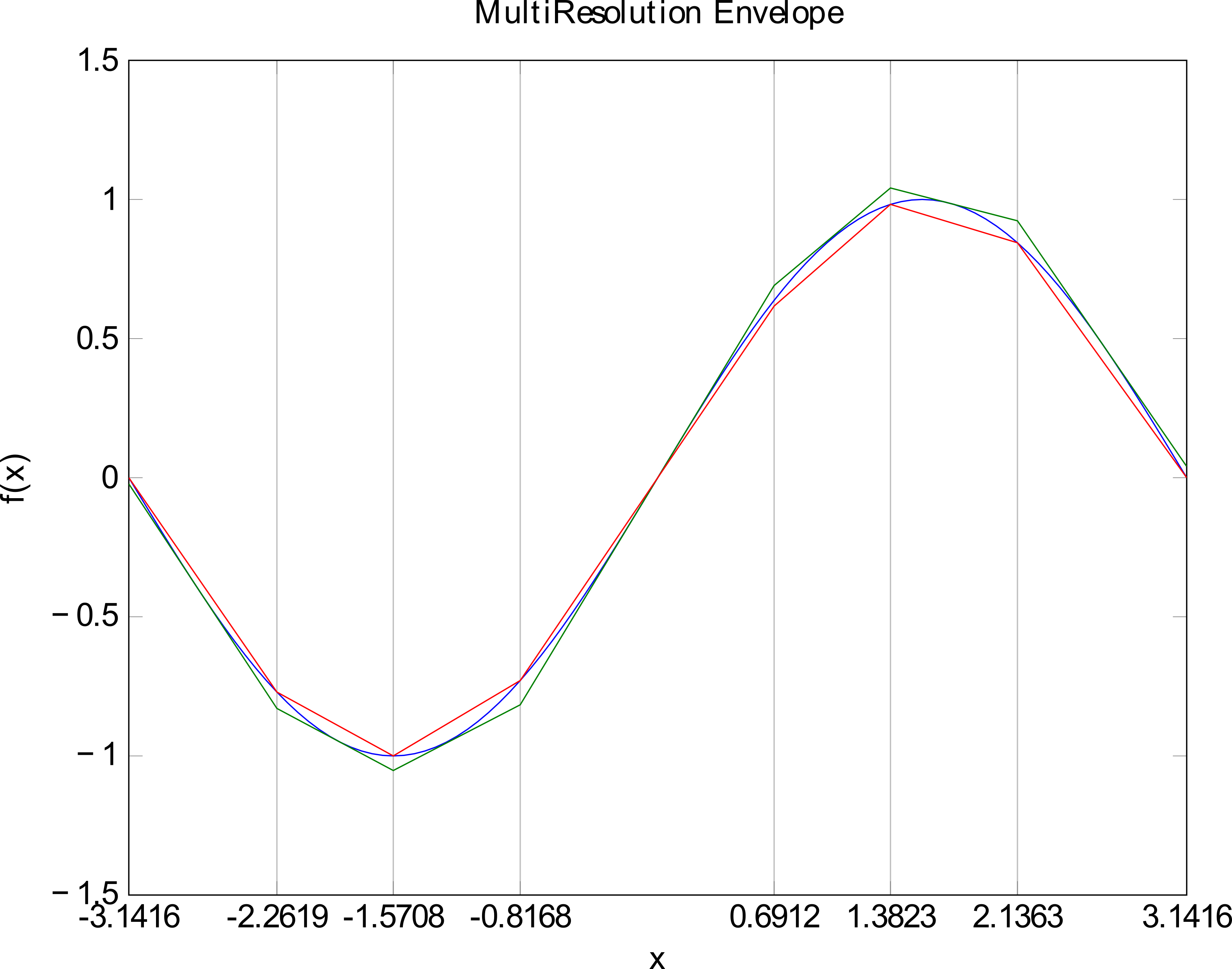
Envelope: computing an "upper" and a "lower" bound for the nonlinear surface

PWA Approximation - Uniform

PWA Approximation - Optimal Uniform

PWA Approximation - Multi-resolution

PWA Approximation - Envelope

PWA Controller Synthesis

Global Lyapunov function

Find a PWA controller \(u=K_ix+k_i\) such that:

\(V(x)=x^\TR P x>0\)
\(\frac{dV}{dt}<-\alpha V\) for \(\alpha>0\)
the control signal is continuous (optional)
This problem is formulated as a set of Bilinear Matrix Inequalities (BMI).
For PWA slab systems, the problem can formulated as a set of Linear Matrix Inequalities (LMI).

PWA Controller Synthesis

Piecewise quadratic Lyapunov function

Find a PWA controller \(u=K_ix+k_i\) such that:

\(V(x)=x^\TR P_i x+2q_i^\TR x+r_i>0\)
\(\frac{dV}{dt}<-\alpha V\) for \(\alpha>0\)
the Lyapunov function is continuous
the dynamics of the closed loop system is continuous

The dynamics of the closed loop system is described by:

\begin{equation*} \dot x = (A_i+B_iK_i)x+a_i+B_ik_i \end{equation*}

The same inequalities are used assuming that the controller known. The BMIs become LMIs.

Example

Flutter Phenomenon

Mechanism of Flutter
1. Inertial Forces
2. Aerodynamic Forces ( \(\propto V^2\) ) (exciting the motion)
3. Elastic Forces (damping the motion)
Flutter Facts
1. Flutter is self-excited
2. Two or more modes of motion (e.g. flexural and torsional) exist simultaneously
3. Critical Flutter Speed, largely depends on torsional and flexural stiffnesses of the structure

[flutter96]

Flutter Suppression

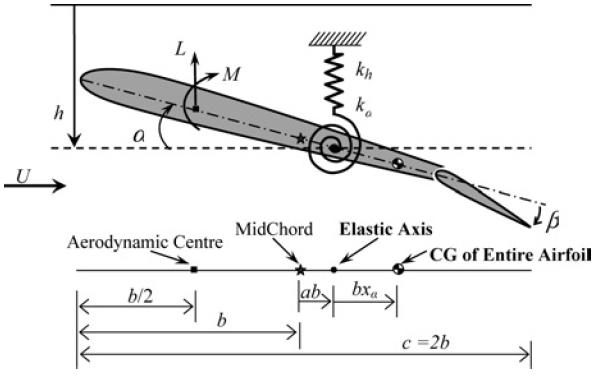
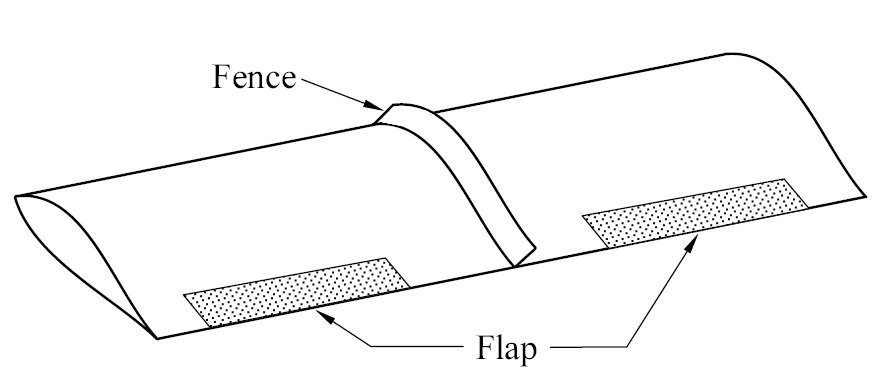
State Space Equations:

\begin{align*} M\bmat \ddot{h} \\ \ddot{\alpha} \emat +(C_0+C_\mu)\bmat \dot{h} \\ \dot{\alpha} \emat+(K_0+K_\mu)\bmat h \\ \alpha \emat+\bmat 0 \\ \alpha K_\alpha(\alpha)\emat=B\beta^o \end{align*}

\begin{equation*} K_\alpha(\alpha)=2.82\alpha-62.322\alpha^2+3709.71\alpha^3-24195.6\alpha^4+48756.954\alpha^5 \end{equation*}

State variables: plunge deflection ( \(h\) ), pitch angle ( \(\alpha\) ), and their derivatives ( \(\dot h\) and \(\dot \alpha\) )
Inputs: angular deflection of the flaps ( \(\beta^o\in\RE^2\) )
Constraints: on states and actuators

[flutter07] [flutter98]

PWATOOLS

Create the system description (4 state variables, 2 inputs):

pwacreate(4,2,’ActiveFlutter_non.m’);

Edit the system description: ActiveFlutter_non.m

model.A = [0 0 1 0;
0 0 0 1;
-M\(Ko+Ku) -M\(Co+Cu)];
model.Bx = [0 0; 0 0;muu*inv(M)*B];
model.aff = [0;0;0;0];
model.fx = @Flutter_Nonlinearity;
model.xcl = [0;0;0;0];
model.Domain ={[-1 1],[-1 1],[-1 1],[-5 5]}
model.NonlinearDomain = [0;1;0;0];
model.mtd = ’Uniform’;
model.M =6; % Number of regions

PWATOOLS

Create the nonlinear function:

function F = Flutter_Nonlinearity(x)

qx2 = 2.82*x(2)-62.322*x(2)^2+3709.71
   *x(2)^3-24195.6*x(2)^4
   +48756.954*x(2)^5;|
M = [12.387 0.418; 0.418 0.065];                                            |
F = [0;0;-inv(M)*[0;qx2]];

Run the system description: ActiveFlutter_non.m. It created two objects:
- nlsys: the nonlinear system
- pwainc: the PWADI

PWATOOLS

Set the design parameters:

x0=[.4 .63 .5 1.2]';
setting.alpha=.1;
setting.SynthMeth='bmi';
setting.RandomQ= 0;
setting.RandomR= 0;

setting.QLin= 1.0e+003 *
[2.7378    1.9536    2.1565    1.5109
1.9536    1.8326    1.5729    0.8522
2.1565    1.5729    1.9228    1.2733
1.5109    0.8522    1.2733    1.1032];

setting.RLin= 1.0e+003 *
[2.7512    3.0551
3.0551    3.3928];

PWATOOLS

Run the controller synthesis command:

ctrl=pwasynth(pwainc, x0, setting);

PWA Controller:

\begin{align*} \overline{K}_1=& \bmat -2.14 & 64.26 & -5.54 & -18.41 & 17.92\\ 2.06 & -61.22 & 2.90 & 6.43 & -7.79 \emat,\\ \overline{K}_2=& \bmat -2.14 & -15.79 & -5.54 & -18.41 & 0\\ 2.06 & 5.39 & 2.90 & 6.43 & 0 \emat,\\ \overline{K}_3=& \bmat -2.14 & -2.59 & -5.54 & -18.41 & 0\\ 2.06 & -28.19 & 2.90 & 6.43 & 0 \emat,\\ \overline{K}_4=& \bmat -2.14 & 77.35 & -5.54 & -18.41 & 26.64\\ 2.06 & -70.89 & 2.90 & 6.43 & -14.24 \emat,\\ \overline{K}_5=& \bmat -2.14 & 85.10 & -5.54 & -18.41 & -48.41\\ 2.06 & -44.49 & 2.90 & 6.43 & 20.10 \emat,\\ \overline{K}_6=& \bmat -2.14 & 40.75 & -5.54 & -18.41 & -18.85\\ 2.06 & -34.06 & 2.90 & 6.43 & 13.15 \emat \end{align*}

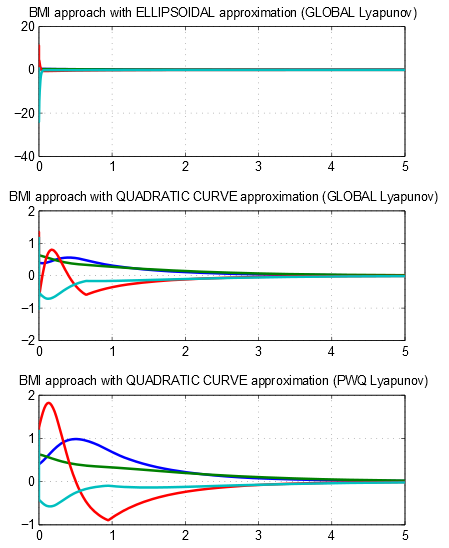
PWATOOLS

Simulation results

Conclusions

PWATOOLS is an easy to use toolbox for PWA systems.
The plan is to extend PWATOOLS algorithms to piecewise polynomial (PWP) systems.
Try PWATOOLS for your problem and let us know how it works.

Publications

1. Rodrigues and J. P. How, "Automated Control Design for a Piecewise-Affine Approximation of a Class of Nonlinear Systems," IEEE American Control Conference, pp.3189-3194, Arlington, Virginia, USA, June 2001
1. Rodrigues and S.P. Boyd, "Piecewise-affine state feedback for piecewise-affine slab systems using convex optimization", 2005, Systems & Control Letters, 54 (9), pp.835-853.
1. Samadi and L. Rodrigues, "Extension of local linear controllers to global piecewise-affine controllers for uncertain nonlinear systems", 2008, International Journal of Systems Science, (39) 9, pp. 867-879.
1. Samadi and L. Rodrigues, "Controller Synthesis for Piecewise-Affine Slab Differential Inclusions: a Duality-Based Approach", 2009, Automatica, 45 (7), pp.812-816.
1. Samadi and L. Rodrigues, "A Unified Dissipativity Approach for Stability Analysis of Piecewise Smooth Systems", 2011, Automatica.

References

[flutter96] Modeling the benchmark active control technology wind tunnel model for application to flutter suppression, M. R. Waszak, AIAA 96 - 3437, http://www.mathworks.com/matlabcentral/fileexchange/3938

[flutter98] Stability and control of a structurally nonlinear aeroelastic system, Jeonghwan Ko and Thomas W. Strganacy, Journal of Guidance, Control, and Dynamics, 21 , 718-725.

[flutter07] Nonlinear control design of an airfoil with active flutter suppression in the presence of disturbance, S. Afkhami and H. Alighanbari, IET Control Theory Appl., vol. 1 , 1638-1649.

[arash98]

Hassibi and S. Boyd. Quadratic stabilization and control of piecewise-linear systems. Proceedings of the American Control Conference, 6:3659 – 3664, 1998

[yalmip]

Löfberg, YALMIP, A Toolbox for Modeling and Optimization in MATLAB, In Proceedings of the CACSD Conference, Taipei, Taiwan, 2004, http://users.isy.se/johanl/yalmip

References

[rodrigues05]

Rodrigues and S. Boyd. Piecewise-affine state feedback for piecewise-affine slab systems using convex optimization. Systems and Control Letters, 54:835–853, 2005

[samadi08]

Samadi and L. Rodrigues. Extension of local linear controllers to global piecewise affine controllers for uncertain non-linear systems, International Journal of Systems Science, 39(9):867–879, 2008

[samadi09]

Samadi and L. Rodrigues, A duality-based convex optimization approach to L2-gain control of piecewise affine slab differential inclusions, Automatica, vol. 45, no. 3, pp. 812 - 816, Mar. 2009

[samadi11]

Samadi and L. Rodrigues, A unified dissipativity approach for stability analysis of piecewise smooth systems, Automatica, vol. 47, no. 12, pp. 2735 - 2742, Dec. 2011

PWATOOLS

A MATLAB Toolbox for Piecewise-Affine Controller Synthesis

M. Zamani, B. Samadi and L. Rodrigues

HYCONS Lab, Concordia University

American Control Conference

Montreal, Quebec

June 2012

Outline

Motivation

PWA Systems

Piecewise Smooth Systems

PWA Systems

PWA Systems

PWA Systems

PWA Slab Systems

PWA Systems

PWA Differential Inclusions

PWA Approximation

PWA Approximation - Uniform

PWA Approximation - Optimal Uniform

PWA Approximation - Multi-resolution

PWA Approximation - Envelope

PWA Controller Synthesis

Global Lyapunov function

PWA Controller Synthesis

Piecewise quadratic Lyapunov function

Example

Flutter Phenomenon

Flutter Suppression

PWATOOLS

PWATOOLS

PWATOOLS

PWATOOLS

PWATOOLS

Simulation results

Conclusions

Publications

References

References